유클리드 기하학의 역사적 배경
유클리드 기하학은 산수, 대수 및 미적분과 같은 분야와 마찬가지로 공리를 바탕으로 발전했습니다. 유클리드 기하학의 공리들을 체계화시킨 고대 그리스인들은 인간의 마음이 물리적 대상과 공간에 대한 기하학적 속성들에 관한 어떤 진리들을 즉각적으로 인식한다고 믿었습니다. 2000년 동안 사람들은 유클리드 기하학 및 수학 일반의 공리들이 물리적 세계에 관한 진리이며 너무나 확실하고 자명한 진리여서 그 누구도 의심할 수 없다고 생각했다.
유클리드 기하학에서 한 평면의 두 직선은 서로 만나지 않으면 평행합니다. 이 명재는 평행선이 존재한다고 주장하지는 않습니다. 하지만 유클리드 기하학에서 평행선의 존재를 암시하는 한 공리가 있습니다. 유클리드가 말한 바에 따르면, 이 공리는 다음과 같습니다.
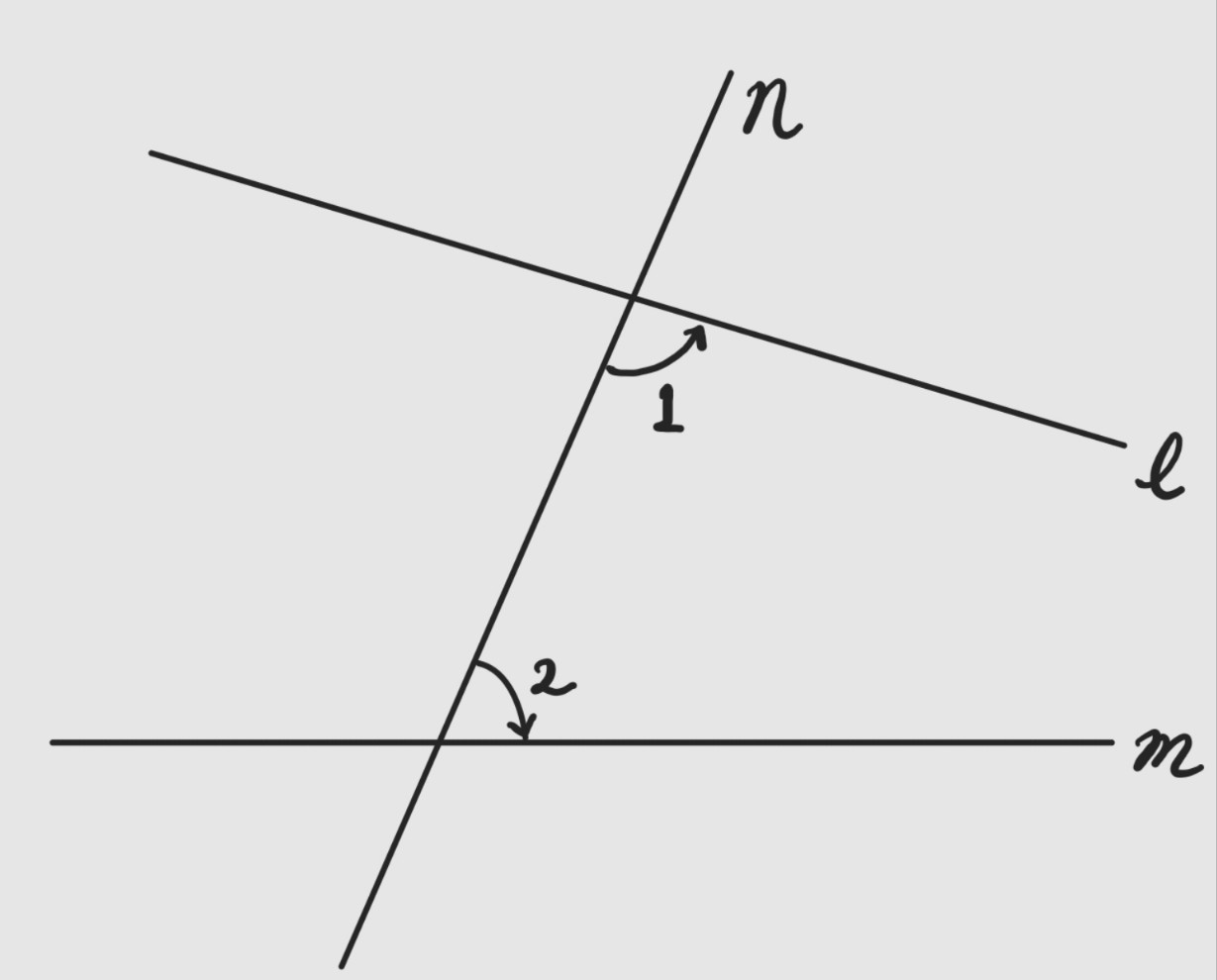
만약 두 직선 l과 m이 직선 n과 만난다면,
각 1과 각 2의 합이 180도보다 작을 경우 각 1과 각 2가 놓여 있는 직선 n의 쪽에서 직선 l과 m이 만난다.
만약 각 1과 각 2의 합이 180도 라면 m과 l이 평행이다.
유클리드는 물론이고 19세기까지의 모든 후대 수학자들도 이 공리가 진리임을 전혀 의심하지 않았습니다. 유클리드 및 그 후예들이 불편해한 것은 이 공리가 다른 공리처럼 자명하지 않다는 것이었습니다. "두 직선이 물리적 공간 속으로 무한정 연장하는데도 서로 만나지 않도록 할 수 있을지 어떻게 확신할 수 있는가? "
18세기가 되자 어떤 수학자들은 새로운 시도를 하였습니다. 유클리드의 공리 집합에는 열 가지 중 평행선 공리를 제외한 아홉 개의 공리로부터 평행선에 관한 공리를 증명하려는 시도였습니다. 하지만 그런 노력은 모조리 실패했습니다.
이런 노력들 중 특별히 주목할 만한 것이 있습니다. 예수회 신부인 지롤라모 사케리는 간접 증명법을 적용했습니다. 유클리드 평행선 공리는 결과적으로, 점 P를 지나며 l에 평행인 직선이 오직 하나 존재한다고 주장합니다. 이 진술이 참인지 모순에 의해 밝기기 위해서는 두 가지 대안이 가능합니다. 첫 번째 점 P를 지나며 l에 평행인 직선이 존재하지 않는다는 진술과 두 번째, 그런 직선이 둘 이상 존재한다는 것입니다. 역사적으로 볼 때, 첫 번째 진술은 모순을 밝혔지만 두 번째 진술은 실패했습니다. 사케리가 이끌어냈어야 했을 결론을 처음으로 내놓은 사람은 최고의 수학자로 불려지는 카를 프리드리히 가우스입니다.
비유클리드 기하학의 탄생
가우스의 가장 위대한 창조물이자 중요한 업적은 그가 내놓은 비유클리드 기하학입니다. 가우스는 어렸을 때부터 이 주제를 생각하기 시작했는데, 이전 사람들과 마찬가지로 유클리드의 평행선 공리를 더 만족스러운 것으로 만들려는 시도였습니다. 하지만 성공하지 못했습니다. 15세 때 친구인 슈마허에게 말한 내용을 보면, 가우스는 평행선 공리를 유클리드의 다른 아홉 공리를 바탕으로 증명할 수 없음을 알고 있었습니다. 가우스는 평행선 공리를 선택하는데 어느 정도 자유가 주어진다면, 유클리드의 공리와는 다른 공리를 선택해도 좋을 것이며 새로운 기하학을 세울 수 있을지도 모른다고 생각했습니다. 가우스는 주어진 한 점을 지나며 한 직선에 평행한 두 개 이상의 평행선이 존재한다는 가정을 포함하는 공리 체계가 어떤 논리적 의미를 지니는지를 연구하여 비유클리드 기하학을 탄생시켰습니다. 가우스는 처음에는 반유클리드 기하학이라고 했다가 이후 별들의 기하학으로 바꾸더니 최종적으로 비유클리드 기하학이라는 용어를 사용했습니다. 가우스는 그런 기하학을 물리적 공간에 적용하는 것을 상상해 볼 수 있으니 정말로 중요한 기하학이라고 인식했지만, 자신의 연구 결과를 발표하지는 않았습니다. 비유클리드 기하학에 관한 가우스의 연구는 1855년 그의 사후에 발견된 논문 속에 들어 있었습니다.
비유클리드 기하학의 창시자로 인정받는 수학자는 연구결과를 직접 발표한 니콜라스 L. 로바체프스키와 보여이 야노시입니다. 로바체프스키는 가난한 집안에서 태어났지만 어렸을 때부터 총명했고 러시아의 카잔 대학교를 다녔습니다. 그의 스승 중에는 독일 수학자 바르텔스가 있었는데 이 사람은 가우스의 친구였습니다. 따라서 평행선 공리의 문제는 바르텔스 덕분에 로바체프스키가 관심을 갖게 되었을 가능성이 높습니다. 로바체프스키는 23세의 나이에 카잔 대학의 교수로 재직하면서 그 문제를 연구했습니다. 1823년에는 유클리드 기하학이 물리적 공간을 꼭 올바르게 기술하는 것이 아니라 다른 기하학이 존재할 수 있음을 깨닫게 됩니다. 로바체프스키는 1829년부터 줄곧 비유클리드 기하학에 담긴 정리들을 설명하는 책과 논문을 발표했습니다. 그는 1846년 교수직에서 해임되었지만, 죽을 때까지 이 분야에 대한 연구를 계속했습니다.
보여이는 헝가리 출신으로 오스트리아의 군 장교였습니다. 그는 아버지인 보여이 볼프강에게서 수학을 배웠는데, 아버지의 권유 덕분에 평행선 공리를 생각하기 시작했습니다. 1823년 보여이는 가우스와 로바체프스키가 도달한 것과 똑같은 결론에 이르렀습니다. 보여이는 1833년에 출간된 아버지의 수학 책에 부록으로 자신의 비유클리드 기하학의 연구 결과를 넣었습니다.
오늘날 로바체프스키와 보여이는 비유클리드 기하학을 최초로 발표했기에 이 분야의 발견자로 인정됩니다. 하지만 1830년대와 1840년대의 수학계는 가우스의 사후에 발견된 논문에서 비유클리드 기하학에 관한 노트가 나오기 전까지 두 수학자의 발표를 무시하였습니다. 수학계에서 이 분야의 적절한 중요성을 얻게 된 까닭도 가우스의 이름이 붙었기 때문입니다. ■
'사소한 수학' 카테고리의 다른 글
| 비유클리드 기하학의 가능성 (0) | 2024.02.06 |
|---|---|
| 곡선 운동을 이해하려면? 매개변수 방정식 (0) | 2024.02.05 |
| 게임과 수학 2탄 (0) | 2024.02.05 |
| 게임과 수학 1탄 (0) | 2024.02.05 |
| 다면체의 신비 2탄 (0) | 2024.02.03 |



