과학 문제를 다루는 수학적 과정, 함수
낙하 물체가 얻는 가속도와 속력과 이동 거리를 각각의 물리적 양에 대해 하나의 식을 사용하여 표현할 수 있습니다. 이는 직선 경로에 따른 운동의 연구입니다. 곡선 경로를 따르는 운동, 가령 날아가는 비행기에서 낙하한 물체의 운동이나 대포에서 발사된 발사체의 운동에 대해 기본 원리를 간파한 사람은 갈릴레오 갈릴레이입니다. 갈릴레오는 직선상의 운동을 다루었던 책인 「두 가지 새로운 과학에 관한 대화」에서 이 운동의 개념과 이를 수학적으로 어떻게 다룰지를 소개하고 있습니다. 곡선 운동을 조사하는 갈릴레오의 목적은 대포알 또는 발사체의 운동을 연구하는 것이었습니다. 14세기에 발명된 대포는 갈릴레오 시대에는 성능이 매우 향상되어서 아주 먼 거리까지 날릴 수 있었습니다. 하지만 발사체 운동의 이론은 갈릴레오 이전에는 잘 알려져 있지 않았습니다. 왜냐하면 수학자들과 물리학자들은 아리스토텔레스의 운동 법칙을 적용하려고 시도했는데, 이 법칙들이 옳지 않았기 때문입니다. 갈릴레오가 다루었던 대포알의 운동 문제는 이후 세기에서 더 중요하게 되었습니다. 날아가는 비행기에서 투하된 폭탄의 운동, 수천 킬로미터를 날아갈 수 있는 무시무시한 발사체의 경로와 유사한 문제들이 갈릴레오가 제시한 방법의 영향력 안에 속하기 때문입니다.
매개변수 방정식의 개념
높은 곳에서 무거운 물체를 수평으로 던진다고 생각해 봅시다. 경험으로 알 수 있듯이 물체는 휘어지며 아래로 떨어집니다. Y축의 양의 방향을 아래쪽으로 잡는 좌표축의 집합을 도입하면, 좌표기하학에서 배운 대로 이 곡선은 하나의 방정식으로 표현할 수 있습니다. 명확한 설명을 위해 이 방정식이
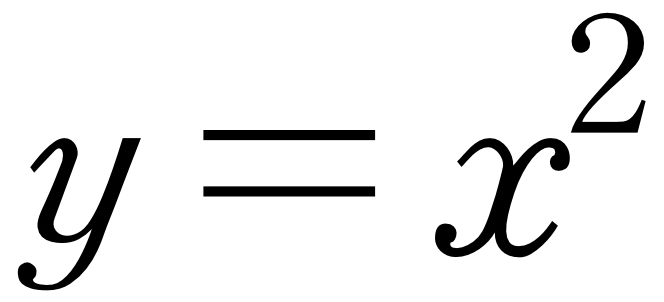
이라고 하겠습니다. 이 식은 x값이 변할 때, y값이 어떻게 변하는지 알려주는 공식입니다. 즉, x와 y사이의 직접적인 관계를 알려주는 공식입니다. 물체가 휘어지면서 아래로 떨어질 때, 공이 점 O에서부터 이동하는 수평 거리와 수직 거리는 시간에 따라 계속 변화합니다. 가령, 이동한 수평 거리가 3일 때는 수직 거리는 9이고, 수평 거리가 4일 때는 수직 거리는 16입니다.
x와 y사이의 직접적인 관계식은 유용할 때가 많지만 물체가 운동할 때의 시간이 빠져 있습니다. 우리는 때때로 물체가 이동한 수평 거리와 시간 사이의 관계 및 수직 거리와 시간 사이의 관계를 알려주는 방정식이 필요합니다. 여기서 물체가 3ft/sec의 속력으로 수평으로 이동한다고 가정하겠습니다. 그렇다면 수평 거리와 시간 사이의 관계를 두 방정식
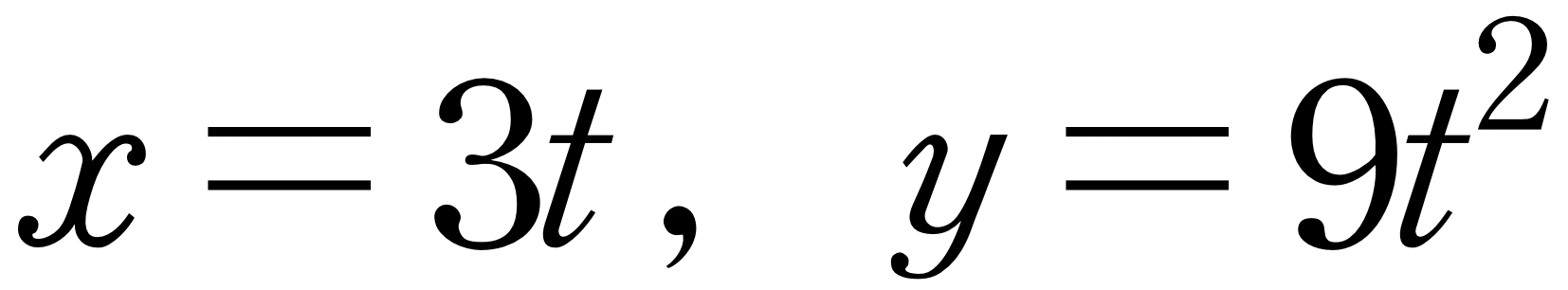
으로 나타낼 수 있습니다. 이 방정식을 곡선의 매개변수 방정식이라고 합니다. 매개변수 방정식은 특정 순간 점의 위치를 지정해 줌으로써 곡선을 표현하는 방식입니다. 좌표평면의 점을 지정하면 평면곡선이 되고 좌표공간의 점을 지정해 주면 공간곡선이 됩니다. 매개변수가 둘 이상이면 곡면을 나타낼 수도 있습니다.
비행기에서 떨어뜨린 발사체의 운동
이제 매개변수 공식이 물리 현상의 연구에 어떻게 쓰이는지 그리고 현상에 관해 새로운 정보를 연역해 내는데 어떻게 유용하게 활용되는지 알아봅시다. 수평 방향으로 시속 60마일의 속력으로 나는 비행기에서 폭탄이 하나 방출된다고 가정해 봅시다. 중력이 없다면 폭탄은 비행기가 나아가는 방향으로 시속 60마일의 속력으로 계속 운동할 것입니다. 이는 운동의 제1법칙의 당연한 결과입니다. 앞서 보았듯이 이 법칙에 의하면, 한 물체가 운동하고 있고 그 운동을 바꾸기 위해 다른 힘이 가해지지 않으면, 한 물체가 원래 갖고 있던 속력으로 무한정 계속 운동합니다. 폭탄은 비행기와 함께 운동하고 있었기에 이미 시속 60마일의 수평 속도를 지니고 있습니다. 우리는 폭탄에 작용하는 다른 힘이 존재하지 않기에 폭탄은 그 속력으로 계속 앞으로 나아갈 것이라고 가정했습니다. 하지만 중력이 작용하고 있으므로, 폭탄이 앞으로 나아가는 것과 동시에 중력이 폭탄을 아래로 끌어당겨 결과적으로 곡선 경로를 만들게 됩니다. 여기서 갈릴레오는 발사체 운동에 적용할 발견을 한 가지 해냅니다. 즉, 수평 운동과 수직 운동을 마치 두 가지가 별도로 일어나고 있는 듯이 연구할 수 있으며, 임의의 순간에 폭탄의 위치는 그것의 수평 이동거리와 수직 이동거리를 찾아내어 알아낼 수 있다는 발견이었습니다. 이 개념은 갈릴레오 시대에는 새롭고 급진적인 것이었습니다. 아리스토텔레스는 한 운동이 다른 운동에 간섭을 일으키므로 임의의 특정한 시간에 오진 한 운동만이 가능하다고 주장했습니다.
갈릴레오의 운동 해석 방법으로 적용해 보면, 폭탄은 시속 60마일, 즉 초속 88피트의 일정한 속력으로 수평으로 운동합니다. 폭탄을 비행기에서 떨어뜨린 순간부터 시간을 재고 아울러 폭탄을 떨어뜨린 점에서의 수평 거리를 재면, t초 후에 폭탄이 이동한 수평 거리 x는 다음 공식이 됩니다.
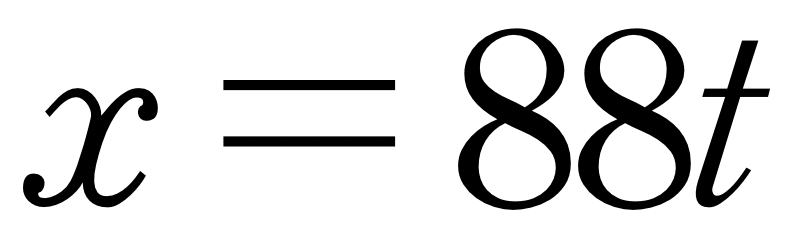
이 공식은 수평 운동을 나타냅니다. 갈릴레오에 따르면, 아래쪽의 수직 운동은 마치 수평 운동과 독립적인 듯이 일어납니다. 하지만 수직 운동은 오직 중력으로 인한 것인데, 알다시피 중력의 작용으로 0의 속력으로 낙하한 물체는 t초 후에 16×t×t의 거리만큼 이동합니다. 따라서 y가 폭탄을 떨어뜨린 지점에서 아래쪽 방향의 거리를 나타낸다면, 다음 식이 얻어집니다.
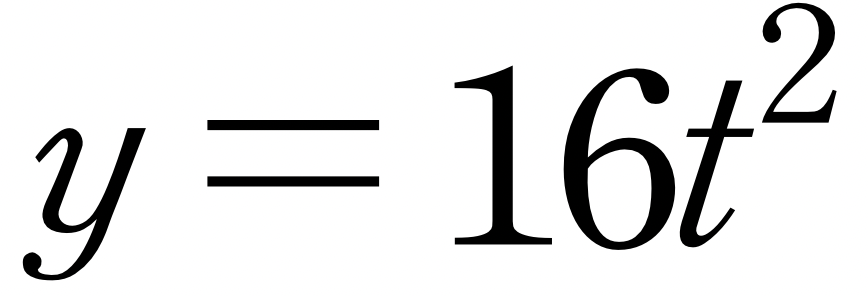
여기서, 수평 이동 거리와 수직이동거리 x, y는 제3의 변수 t에 의해 주어집니다. 이 두 공식은 해당 운동에 대한 매개변수 방정식입니다. 그리고 이 곡선은 포물선임을 알 수 있습니다. 포물선 전체는 Y축의 오른쪽과 왼쪽의 양의 방향으로 뻗어갑니다. 하지만 이 경우에는 오른쪽 부분, 즉 양의 x값에 대응하는 절반만이 폭탄의 운동을 나타냅니다. 그리고 O로부터 지면에까지 이어진 부분만 해당됩니다.
두 비행기가 각각 시속 60마일과 120마일의 속력으로 수평으로 날고 있다고 가정해 봅시다. 이 두 폭탄 중에서 어느 것이 지면에 빨리 닿을까요? 두 비행기의 속력의 차이는 운동에 어떤 영향을 미칠까요? 시속 60마일로 나는 비행기는 폭탄에 시속 60마일, 즉 초속 88피트의 수평 속력을 주며, 시속 120마일로 나는 비행기는 폭탄에 시속 120마일, 즉 초속 176피트의 수평 속력을 줍니다. 따라서 두 폭탄은 서로 다른 수평 속력으로 운동하며, 동일한 시간 t후에 두 번째 폭탄이 첫 번째 폭탄보다 더 멀리 이동합니다. ■
'사소한 수학' 카테고리의 다른 글
| 비유클리드 기하학의 가능성 (0) | 2024.02.06 |
|---|---|
| 비유클리드 기하학의 탄생 (0) | 2024.02.05 |
| 게임과 수학 2탄 (0) | 2024.02.05 |
| 게임과 수학 1탄 (0) | 2024.02.05 |
| 다면체의 신비 2탄 (0) | 2024.02.03 |



