로그는 큰 수의 곱셈을 편리하게 하기 위해 발명되었다
네이피어(J. Napier)는 로그를 구성하는 데 20여 년 이상의 시간 동안 매달린 스코틀랜드의 남작이었습니다. 수학, 신학, 점성술을 좋아하였는데, 특히 신학에서는 슈티펠*(Michael Stifel)처럼 교황이 반 기독교인이라는 사실을 증명하는데 관심이 있었으며, 「성 요한 묵시록 전체에서의 소박한 발견」(A Plaine Discovery of Whole Revelation of St. John)이라는 책을 출판하였습니다. 네이피어가 발견한 것 중에는 1700년 이전에 세상의 종말이 올 것이라는 부분도 있습니다.
* 슈티펠(Michael Stifel)은 독일의 수학자로 처음에는 수도원에 들어갔으나 마르틴 루터의 종교 개혁에 자극을 받아 수도원을 뛰쳐나와 로마교황과 그 권위에 반대하는 한편 수학 연구에 몰두하여 독창적 업적을 세웠습니다. 유리수, 무리수, 대수의 3부로 나누어 쓴 저서 「정수계산」(Aithmetica Integra)에는 파스칼의 삼각형, 음수, 거듭제곱, 거듭제곱근 등의 내용이 담겨있습니다.
언젠가 네이피어의 하인들 중에 도둑질을 한 사람이 있었습니다. 네이피어는 도둑을 잡기 위해 하인들에게 어두운 방으로 한 사람씩 들어가서 영혼의 닭을 만지라고 말하였습니다. 그는 이 수탉은 사람들이 만지면 도둑질 한 사람이 누구인지를 알게 되고, 그 사실을 자신에게 알려줄 것이라고 말합니다. 네이피어는 하인 몰래 그 수탉 몸에 검댕이를 묻혀 놓습니다. 진짜 도둑은 감히 수탉을 만질 수 없어 깨끗한 손으로 나왔습니다.
네이피어는 로그를 계산하는 방법을 1614년에 발표한 저서 「놀라운 로그 법칙의 기술」(Mirigici Logarithmorum Cannonis Construcrio)에서 수록해 놓고 있습니다. 로그(Log)는 Logos + arithmetic의 합성어인 Logarithm의 앞글자를 딴 네이피어가 만든 신조어입니다. 하지만 이 책을 읽기가 쉽지 않습니다. 왜냐하면 네이피어가 x의 로그라 부르는 것이 실제로는
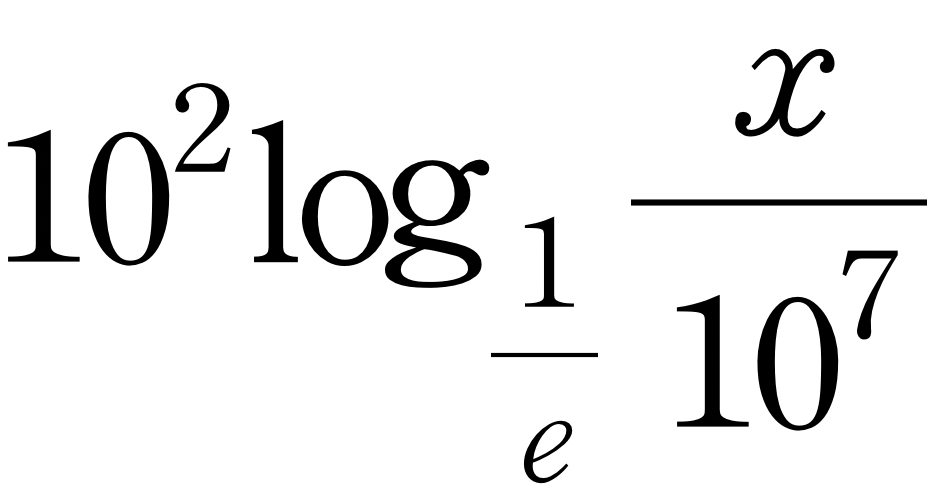
를 의미하기 때문입니다.
또한, 이 책은 오차의 한계에 대하여 상세한 설명을 해놓고 있기 때문에 어렵고 지루합니다. 여기에는 네이피어의 기본적인 아이디어만 소개하겠습니다. 수직선상의 음의 부분에서 원점을 향하여 원점으로부터의 거리에 비례하는 속도로 움직이는 미립자가 있다고 하면, 시간 0에서 미립자는 -1 지점에 있습니다. 거리 d에 대하여, 미립자가 원점으로부터 떨어진 거리 d에 대응하는 시간이 있습니다. 이 시간을 d의 로그라 정의합니다.
쉽게 설명하면 다음 식에서 미지수인 지수를 로그라고 부릅니다.
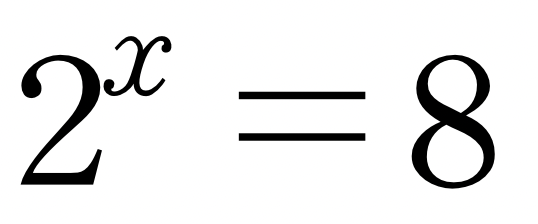
에서 x는 2를 밑으로 하는 8의 로그입니다. 이렇게 말로 표현하면 다소 길어지기 때문에 줄여서

과 같이 씁니다.
로그는 곱셈을 덧셈으로 쉽게 해결해 준다
16X32=512 같은 곱셈을
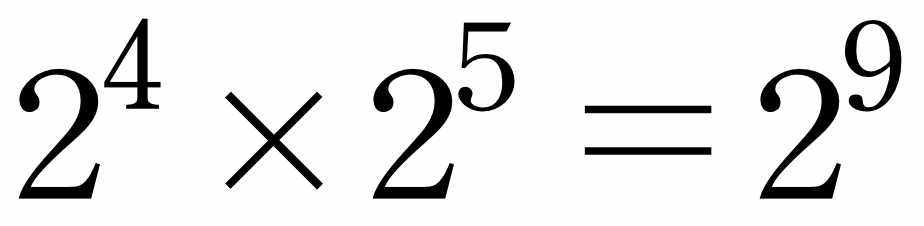
으로 다시 씀으로써 그 계산을 단순히 지수끼리 더하는 4+5=9 식으로 편하게 바꿀 수 있다고 생각해 봅시다. 계산기가 나오기 전에, 공학자나 기술자들은 두 수를 곱할 때 두 수의 로그값을 표에서 찾아서 더한 다음 표에서 그 합을 찾는 식으로 답을 구했습니다. 이렇게 하는 편이 손으로 계산하는 것보다 빠른 경우가 많았고, 계산자*도 바로 이런 원리를 기반으로 만들어진 도구입니다.

*공학자들은 계산자를 사용해 겨우 몇 초 만에 곱셈과 나눗셈을 완료하고 제곱근을 찾아내는 것을 비롯해 아주 많은 일들을 할 수 있었습니다. 1621년에 최초 형태의 계산자를 발명한 인물은 영국 수학자이자 성공회 목사인 윌리엄 오트레드였는데, 그 기반이 된 것은 스코틀랜드 수학자인 존 네이피어의 로그였습니다.
상용로그의 탄생, 그 활용
영국의 수학자 헨리 브리그스(Henry Briggs)는 네이피어가 로그를 발견하자 그 중요성을 인정하여 1615년에 에든버러로 네이피어를 찾아갑니다. 그 둘은 밑을 10으로 하는 로그가 여러 가지로 편리하다는 점에 의견의 일치를 보게 됩니다. 그 후 공동으로 로그의 기본 부분을 수립하게 됩니다. 1617년, 네이피어가 죽었지만 브리그스는 그 연구를 계속하였습니다. 1624년에 저서 「로그산술」(Arithmetica Logarithmica)에 1부터 2만까지, 9만부터 10만까지의 14자리 대수를 10의 거듭제곱 꼴로 바꾸어 놓은 로그표를 발표합니다. 10을 밑으로 하는 상용로그를 흔히 '브리그스 로그수'라고 부르는 까닭은 이 때문입니다.
오늘날 과학에서는 다양한 값들이 로그를 사용하여 표시됩니다. 예를 들어 화학에서 사용하는 산성 농도 단위인 ph, 음향에서
소리의 세기를 나타내는 벨 단위를 측정할 때, 지진의 규모를 측정하는 리히터 규모 같은 것들은 모두 밑을 10으로 하는 로그를 사용합니다.
로그법은 복잡한 계산들을 할 수 있게 해 주어 과학과 공학의 수많은 진보에 공헌했습니다. 전자계산기를 쉽게 이용할 수 있게 되기 전까지 조사와 항해에 로그와 로그표들이 흔히 이용되었습니다. 또한, 네이피어는 '네이피어의 뼈(Napier's Bones)'도 발명했는데, 이것은 계산을 보조하는 곱셈표들이 새겨진 막대입니다. ■
'사소한 수학' 카테고리의 다른 글
| 파스칼은 천재? , 정신이상자? (0) | 2024.02.01 |
|---|---|
| 기하학에 새로운 방법, 데카르트의 좌표기하학 (0) | 2024.02.01 |
| 위대한 술법(Ars Magna)이 현대대수학의 탄생에 끼친 영향 (2) | 2024.02.01 |
| 조립제법(Synthetic division)의 원리 (0) | 2024.02.01 |
| 복소수의 등장 (0) | 2024.02.01 |



