다항식에 대한 호제법(Division Algorithm)
두 정수의 최대공약수를 체계적으로 구하는 방법인 정수에 관한 유클리드 호제법은 정수를 다루는 데 기본적으로 활용되는 정수의 호제법을 근간으로 하고 있습니다.
즉, 정수 a를 양의 정수 b로 나누면 몫과 나머지가 얻어지는데, 특히 나머지는 b의 크기보다 작은 범위에서 얻어진다는 것입니다. 이러한 정수의 호제법은 다항식의 호제법으로 응용되어 방정식의 해집합을 구하는데 유용하게 활용되기도 합니다.

이러한 q(x)와 r(x)는 f(x)를 g(x)로 나눌 때의 몫(quotient)과 나머지(remainder)라고 각각 부릅니다.
이 정리에서 r(x)=0 이면 f(x)=q(x) g(x)가 되는데, 이때 f(x)는 g(x)의 배수(multiple) 그리고 g(x)는 f(x)의 약수(divisor) 또는 인수(factor)라고 부릅니다.
공약수와 나머지정리
다항식에 대한 호제법에서 나머지가 0인 경우는 특별히 중요한 여러 가지 성질들이 있습니다. 이는 산술의 기본정리나 정수에 관한 많은 성질들이 소수의 성질에서 비롯되기 때문에 정수에서 1보다 큰 정수가 소수인지 안닌지를 구분하는 것이 중요하게 다루어지는 것처럼 다항식에 관한 이론에서 중요한 역할을 합니다.
다항식의 호제법에서 주어진 다항식을 일차다항식으로 나누는 특별한 경우에는 나머지정리와 인수정리가 얻어지는데 이 두 정리는 주어진 다항식의 가약성(reducibility)에 대한 성질을 알게 해 줍니다.
나머지 정리(Remainder Theorem)는 다음과 같습니다.
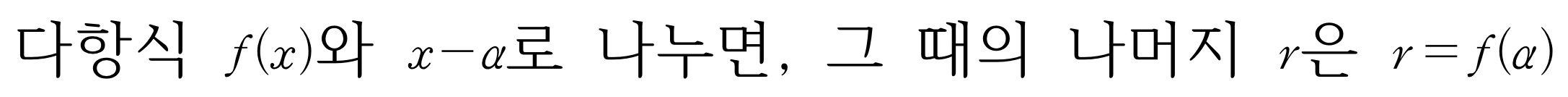
나머지정리는 하나의 주어진 다항식을 다항식으로 나누었을 때 나머지를 구할 수 있는 방법이고, 조립제법은 인수가 다항식일 때 위와 같은 나눗셈을 간단히 하는 방법입니다.
조립제법
다음의 예를 생각해 봅시다.
다항식
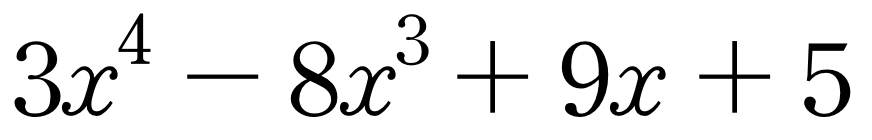
를
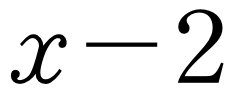
로 나누면
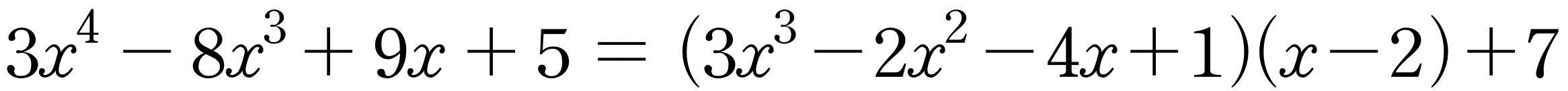
를 얻는데, 이는 다음과 같은 계산과정에서 얻게 된 것입니다.
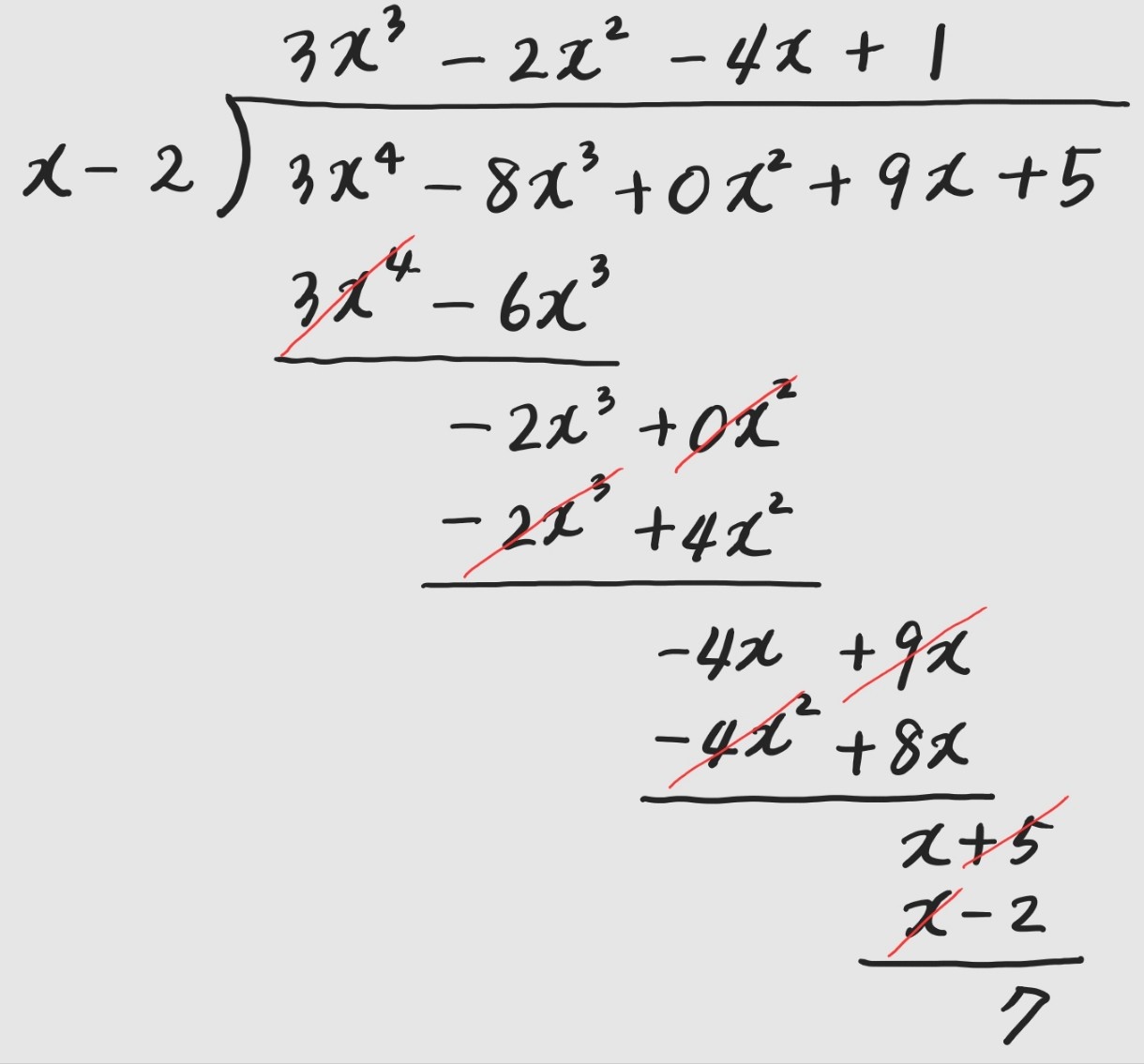
앞과 같은 계산과정은 아주 간단한 문제의 성질에 비추어 볼 때 너무나도 많은 노력이 요구된다고 할 수 있습니다. 따라서 이러한 표기들을 간단히 하는 방법을 생각해 봐야 합니다. 우선 위의 계산과정 속에서 수직으로 들어있는 x의 거듭제곱을 가지고 있는 항을 정리하고, x는 생략해도 괜찮습니다. 또한 그대로 내려올 수 있는 항도 마찬가지로 생략할 수 있습니다. x의 거듭제곱 중에서 빠진 부분의 계수를 0이라 한다면 위의 과정은 다음과 같이 간단히 쓸 수 있습니다.
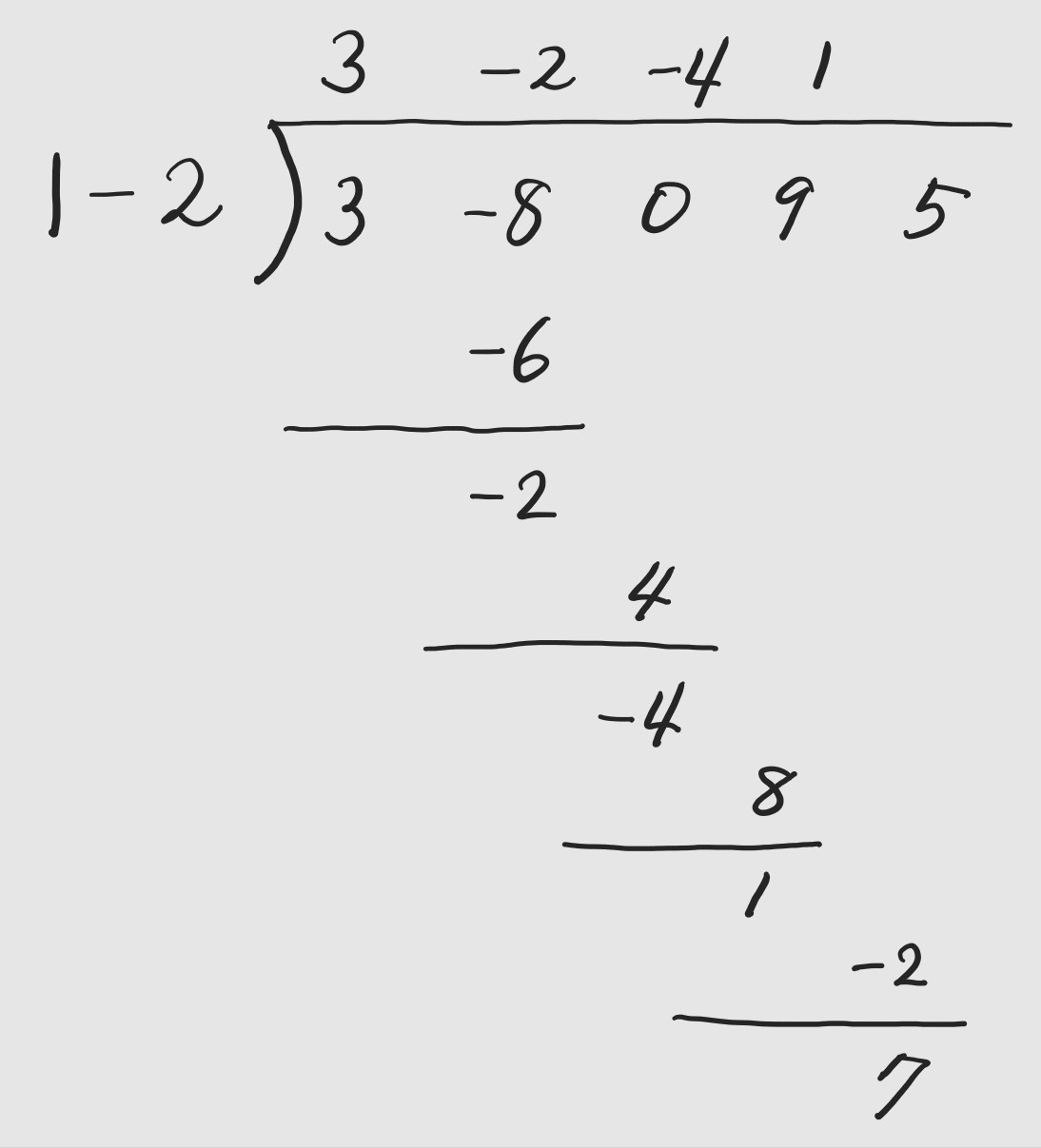
그런데 인수의 x의 계수가 1이므로 계수 1을 생략할 수 있습니다. 더욱이 우리의 표현방식을 조금 더 완성도를 갖추도록 써보기 위하여 아래쪽에 늘여서 쓴 숫자들을 옮겨 적습니다.

이러한 과정에 있어서 맨 아래 줄의 첫 번째 자리에 최고차의 계수 3을 도입하여 쓰면 마지막 줄의 앞에서부터 네 번째까지의 수인 3, -2, -4와 1은 몫의 계수이고 마지막 숫자 7은 나머지가 됩니다. 그리고 몫의 계수를 두 번씩 쓸 필요가 없으므로 위의 과정에서 첫 번째 줄은 생략하기로 하면 다음을 얻을 수 있습니다.
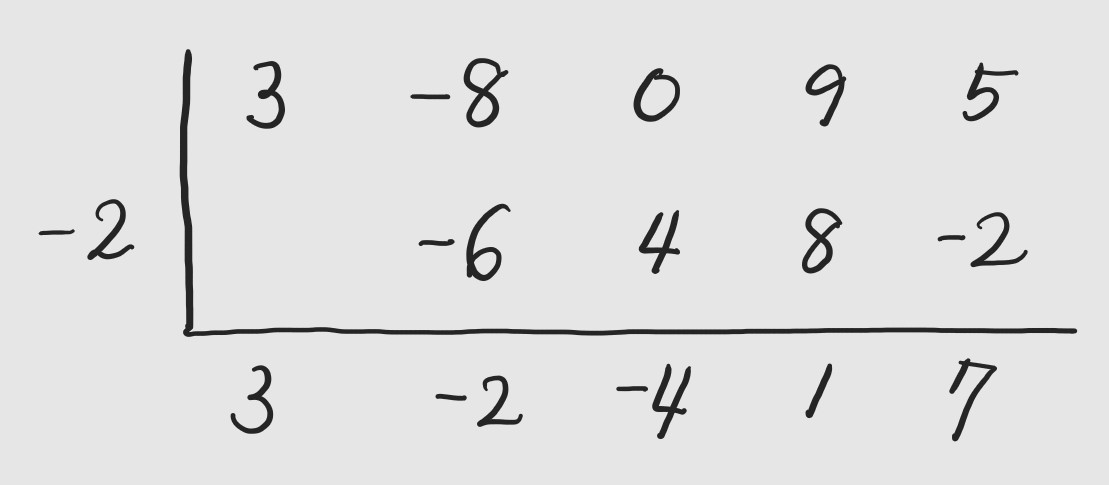
이러한 과정을 다시 설명해 보면 다음과 같습니다. 두 번째 줄의 각 원소는 세 번째 줄에 들어있는 바로 앞의 원소에 -2를 곱한 결과이고 세 번째 줄의 각 원소는 첫 번째 줄에서 두 번째 줄을 뺀 결과입니다. 바로 이러한 셈법은 구체적인 나눗셈의 과정을 거치지 않아도 계산 과정을 수행할 수 있는 방법입니다. 다항식의 항을 x의 내림차순으로 정리하고 계수들을 한 줄로 늘어놓는데 빠진 차수가 있는 경우에는 그 계수를 0으로 하여 씁니다. 그런 다음에 그 줄의 맨 왼쪽에 -2를 쓰고 최고차 항의 계수 3을 세 번째 줄의 맨 처음으로 내려보냅니다. 그러고 나서 3과 -2를 곱하여 두 번째 줄의 첫 번째 원소-6을 구하여 쓰고 -8에서 -6을 빼면 -2가 세 번째 줄의 원소가 됩니다. 마찬가지 방법으로 -2에 -2를 곱해서 두 번째 줄의 두 번째 원소 4를 구하고 0에서 4를 빼서 얻은 수 -4를 세 번째 줄의 세 번째 원소로 하는 이러한 과정을 세 번째 줄의 마지막 원소를 얻을 때까지 계속합니다. 이와 같은 과정에서 -2 대신에 2를 사용하면 두 번째 줄의 원소의 부호가 바뀌는데 이 경우에는 세 번째 줄의 원소를 구하기 위해서 첫 번째 줄과 두 번째 줄의 원소를 각각 대응되는 것들끼리 더하면 됩니다.
이와 같은 계산 방법을 조립제법(Synthetic division)이라고 합니다.
조립제법은 다항식을 직접 나누지 않고 그 계수만을 이용하여 나눗셈을 하여 몫과 나머지를 구할 수 있는 방법입니다. 긴 다항식을 나눌 때 다항식의 계수만 조립하여 나눗셈을 하는 방법을 말하는데 1804년 이탈리아의 수학자 루피니(Paolo Ruffini)가 처음 발견했습니다. 나머지 정리는 나머지를 쉽게 구할 수 있게 하지만 그 몫을 구해 주지는 못합니다. 반면에 조립제법은 나머지뿐 아니라 몫까지 쉽게 구할 수 있는 이점이 있습니다. 조립제법은 다항식 f(x)에 대하여 한 근을 알 경우, 그 근으로 나눈 몫을 쉽게 구할 수 있게 합니다. 이를 이용하여 방정식의 근을 찾는 방법을 수학자 호너(William George Horner)의 방법이라고 합니다. 호너의 방법은 조립제법의 본질이어서, 일반적인 조립제법을 호너의 방법이라고 하기도 합니다. ■
'사소한 수학' 카테고리의 다른 글
| 새로운 계산 도구, 로그 (0) | 2024.02.01 |
|---|---|
| 위대한 술법(Ars Magna)이 현대대수학의 탄생에 끼친 영향 (2) | 2024.02.01 |
| 복소수의 등장 (0) | 2024.02.01 |
| 부등식, 절대부등식-조건부부등식 (0) | 2024.01.31 |
| 수학적 귀납법(Mathematical induction) 이란? (0) | 2024.01.30 |



