수학자들의 대수학 연구
카르다노(G. Cardano)가 1545년에 발표한 위대한 술법(Ars Magna)이라는 저서 속에 들어 있는 여러 가지 발견 중에서 가장 중요한 소득의 하나는 수학자로 하여금 다양한 방법으로 대수학을 연구하도록 하게 하였다는 점입니다. 즉, 임의의 차수를 갖는 방정식의 해법을 생각하는 쪽으로 연구가 일반화되었는데, 특히 오차방정식의 대수적인 해법을 생각하도록 하였습니다. 이후로 2세기 동안이나 수학자들은 고대의 고전적인 기하문제와 비교되는 풀리지 않는 대수적 문제를 다루게 됩니다.
무리수는 카르다노 시대에도 비론 이론적인 기초가 빈약하기는 하였지만 유리수의 근삿값으로 받아들여졌습니다. 그러나 음수의 경우는 당시에도 받아들여지기가 쉽지 않았었습니다. 따라서 어떤 대수학자가 무리수나 음수의 존재를 부인한다면 그러한 사람들은 다음과 같은 식의 해는 없다고 생각해 버릴 수 있는 것입니다.
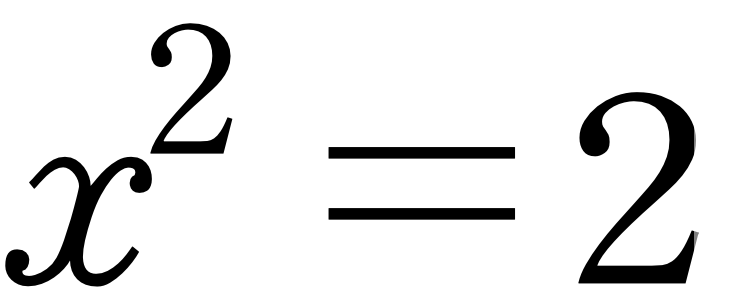
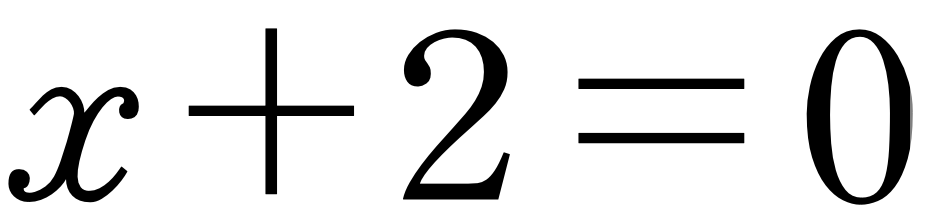
그러나 일반적으로 삼차방정식의 해에는 카르다노의 해법에 의하여 음수의 제곱근이 등장하게 됩니다. 그와 같은 수는 기존에 알고 있던 수와는 전혀 다른 수이고, 이렇게 하여 등장하게 된 것이 복소수입니다.
복소수의 등장
만일 어떤 수 a가 실수라면, a의 제곱은 음의 실수가 될 수 없다는 사실로부터 제곱해서 -5가 되는 수는 실수의 범위에서 존재하지 않음을 알 수 있습니다. 따라서 이러한 방정식의 해로 이루어진 새로운 수체계 C를 만들 필요가 생겨나는데, 이 새로운 수체계 C는 먼저 실수의 집합 R을 부분집합으로 포함하여야 하고, 실수의 경우와 마찬가지로 덧셈과 곱셈의 연산이 정의되어야 합니다. 또한 이러한 새로운 수체계의 연산들은 범위를 실수로 제한하였을 때에는 실수에서의 연산과 일치하도록 만들어져야 합니다. 이를 위하여 직관적인 방법을 살펴보면 다음과 같이 생각할 수 있습니다. 먼저 k가 실수라고 할 때,
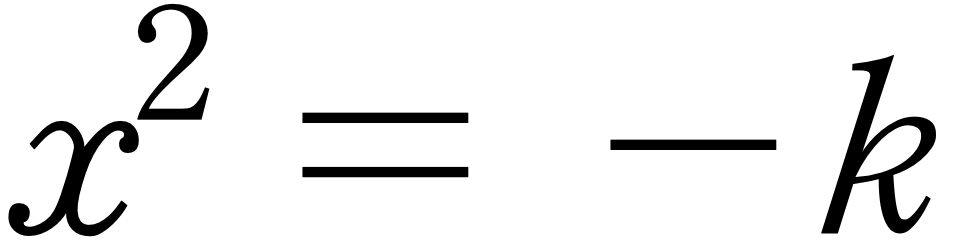
의 해가 k=1 일 때 적당한 i 가 존재한다는 것과 같습니다.
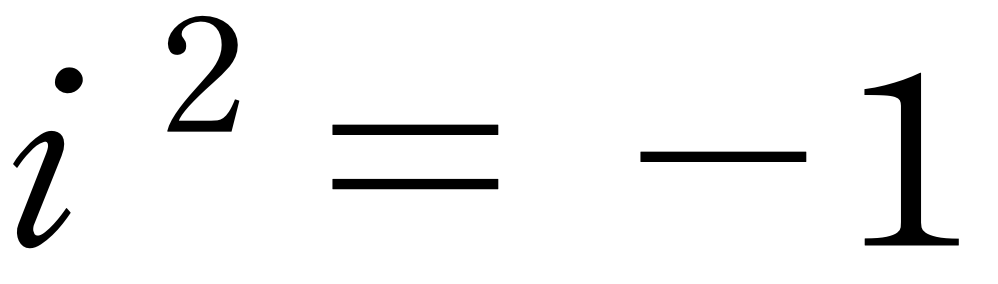
또, b가 실수라고 하면 이 b는 새로운 수 체계 C안에 속하고 C가 곱셈에 관하여 닫혀있다면
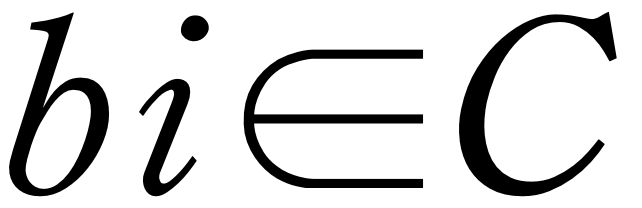
이어야 합니다.
더욱이 a가 실수이고 C가 곱셈에 관하여 닫혀있다면
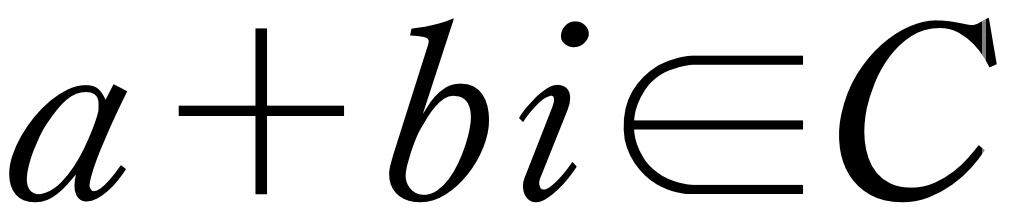
이어야 합니다.
이때,
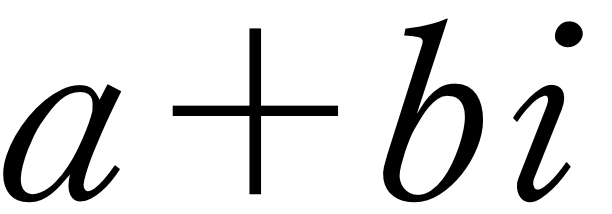
을 복소수(Complex number)라고 부릅니다.
복소수, 수학자들의 재앙
복소수는 18세기의 수학자들에게 재앙 이상이었습니다. 복소수는 카르다노에 의하여 알려지게 된 이후 1700년경까지 수학자들에 의하여 무시되었습니다. 오일러(Euler)도 복소수가 무엇인지 이해하려 애썼으나 상상 속에나 존재하는 수라고 생각하여 상상 속의 수(imaginary number) 또는 환상의 수(fancied number)라고 불렀습니다. 왈리스(John Wallis)는 1685년에 출간된 대수학이라는 저서에서 실계수 이차방정식의 복소수 근을 기하학적으로 나타내는 방법을 제시하였습니다. 그의 방법은 옳은 방법이기는 하였으나 여러 가지 목적에 맞는
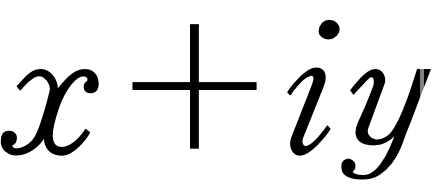
의 유용한 표현이라고 할 수는 없었습니다. 그러나 복소수의 기하학적은 표현은 노르웨이의 베셀(Casper Wessel), 스위스의 아르강(Jean Robert Argand) 등을 거쳐 가우스에 의하여 완성하게 되었습니다.
실수의 순서쌍 좌표평면 상의 한 점으로 생각할 수 있으므로 복소수의 집합 C는 x좌표를 실수축(real axis), y좌표를 허수축(imaginary axis)으로 하는 복소평면(complex plane) 또는 가우스평면(Gaussian plane) 상의 점의 집합으로 생각할 수 있게 됩니다. 이제 복소평면상의 한 점 P(x, y)가 원점 O에서 실수축과 허수축에 대하여 각각 x, y인 좌표를 갖고, 실수축과 역시계방향으로 이루는 각을 ∂, 원점 O로 부터 점 P(x, y)까지의 거리를 r이라 하면,
x = r cos∂ , y = r sin∂
로 쓸 수 있으므로
z = x + yi = r ( cos∂ + i sin∂ )
로 쓸 수 있는데, 이를 복소수의 삼각함수형식(trigonometric form) 또는 극형식(polar form)이라고 부릅니다.
이때, r은 원점 O에서 점 P(x, y)까지의 거리이므로
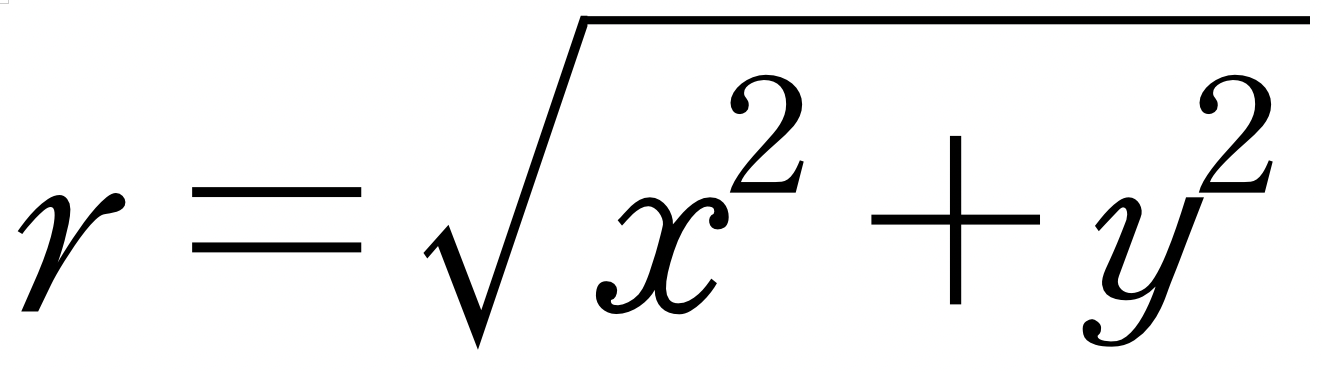
입니다. 이러한 복소수의 극형식은 유일하다고 할 수 없는데, 그 이유는 각 ∂를 무수히 많이 선택할 수 있기 때문입니다.
복소수의 벡터표시
벡터라는 말은 라틴어 vectus라는 용어에서 비롯되었는데 이는 옮긴다는 의미입니다. 즉, (0, 0)이라는 지점에서부터 (3, 4)까지 옮기게 되면 그렇게 옮기는 것을 하나의 벡터로 나타낼 수 있다는 것입니다. 복소수를 벡터로 표시한 것은 물리학의 응용에 활용됩니다. 왜냐하면 물리학자들에게 있어서 하나의 벡터란 힘이나 속도 또는 가속도와 같이 크기와 방향이 있는 하나의 실체를 의미하기 때문입니다.
유향선분(directed line segment)이라 함은 방향을 가진 선분으로써 벡터(vector)라고도 부릅니다. 어떤 벡터가 출발점은 A, 끝점을 B로 하고 있다면 이러한 벡터를

라고 씁니다. 벡터들은 크기나 방향을 바꾸지 않고 하나의 위치로부터 다른 위치로 옮길 수 있는데 이러한 벡터를 자유벡터(ㄹfree vector)라고 합니다. 물리적인 많은 개념들이 벡터로 표현될 수 있습니다.
예를 들어 한 비행기가 수평선으로부터 20도의 각도로 시속 100마일의 속도로 착륙 중인 벡터를 v로 표시하기로 한다면, 이러한 벡터 v를 속도벡터(velocity vector)라고 합니다. 그러면 v의 크기 ㅣvㅣ는 비행기의 속력을 의미하는 것이 됩니다.
두 번째 예로 어떤 사람이 5킬로그램이 되는 물건을 위로 들어 올린다고 합시다. 그러면 이러한 사실은 힘 F로 물건을 들어올리는 것을 나타낼 수 있습니다. 이와 같이 물체에 가해지는 힘을 나타내는 벡터를 힘 벡터(force vector)라고 합니다.
벡터의 합은 우리가 자유벡터를 대상으로 하여 생각한 거이므로 임의의 벡터에 대하여도 한 벡터의 출발점과 또 다른 벡터의 끝점이 일치하기만 하면 그대로 적용할 수 있습니다. ■
'사소한 수학' 카테고리의 다른 글
| 위대한 술법(Ars Magna)이 현대대수학의 탄생에 끼친 영향 (2) | 2024.02.01 |
|---|---|
| 조립제법(Synthetic division)의 원리 (0) | 2024.02.01 |
| 부등식, 절대부등식-조건부부등식 (0) | 2024.01.31 |
| 수학적 귀납법(Mathematical induction) 이란? (0) | 2024.01.30 |
| 변수를 이용하여 얻을 수 있는 다항식과 대수식 (0) | 2024.01.30 |



